Var X Again Your Answer Should Be in Terms of P

Contents:

1. What is Expected Value?
2. Formula
   • Bones Formula
   • Binomial Random Variable
   • Multiple Events
   • Expected Value for Continuous Random Variables
   • Expected Value Formula for an Capricious Office
3. Find an Expected Value by Hand
4. Find an Expected Value in Excel
5. Observe an Expected Value for a Discrete Random Variable
6. What is an Expected Value used for in Existent Life?
7. St. Petersburg Paradox

What is Expected Value?

Expected value is exactly what you lot might recollect it ways intuitively: the render you can wait for some kind of action, like how many questions you might get right if you guess on a multiple selection test.

Picket this video for a quick caption of the expected value formulas:

Can't see the video? Click here.

For instance, if you take a xx question multiple-pick exam with A,B,C,D as the answers, and you guess all "A", then you tin can wait to become 25% correct (5 out of 20). The math behind this kind of expected value is:
The probability (P) of getting a question right if you guess: .25
The number of questions on the test (n)*: xx
P x n = .25 x twenty = v

*You might see this as X instead.

This type of expected value is chosen an expected value for a binomial random variable. It's a binomial experiment because there are only two possible outcomes: you become the answer right, or you get the answer wrong.

Formula

Basic Expected Value Formula

The basic expected value formula is the probability of an event multiplied by the amount of times the outcome happens:
(P(x) * north).

The formula changes slightly according to what kinds of events are happening. For most simple events, you lot'll use either the Expected Value formula of a Binomial Random Variable or the Expected Value formula for Multiple Events.

Formula for the Expected Value of a Binomial Random Variable

The formula for the Expected Value for a binomial random variable is:
P(10) * X.
Ten is the number of trials and P(10) is the probability of success. For instance, if you toss a coin ten times, the probability of getting a heads in each trial is 1/ii so the expected value (the number of heads you can expect to get in 10 money tosses) is:
P(10) * X = .5 * 10 = 5

Tip: Summate the expected value of binomial random variables (including the expected value for multiple events) using this online expected value estimator.

Expected Value for Multiple Events

Of course, computing expected value (EV) gets more than complicated in real life. For example, You buy one $10 raffle ticket for a new car valued at $15,000. Two grand tickets are sold. What is the EV of your proceeds? The formula for computing the EV where there are multiple probabilities is:

E(X) = ΣX * P(X)
Where Σ is summation annotation.

The equation is basically the same, but here yous are adding the sum of all the gains multiplied by their individual probabilities instead of just one probability.

Other Expected Value Formulas

The two formulas higher up are the 2 virtually mutual forms of the expected value formulas that you'll see in AP Statistics or elementary statistics. Even so, in more rigorous or avant-garde statistics classes (like these), you might come up across the expected value formulas for continuous random variables or for the expected value of an arbitrary role.
Expected Value Formula for an Arbitrary Office

Expected Value for Continuous Random Variables

The expected value of a random variable is merely the mean of the random variable. You tin summate the EV of a continuous random variable using this formula:

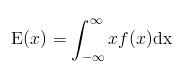
Expected value formula for continuous random variables.

Where f(ten) is the probability density role, which represents a function for the density bend.
The "∫" symbol is chosen an integral, and it is equivalent to finding the area under a curve.

Expected Value Formula for an Capricious Function

If an event is represented by a part of a random variable (1000(x)) and so that function is substituted into the EV for a continuous random variable formula to get:

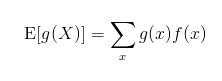
Expected value formula for an arbitrary function.

Back to Pinnacle

Calculate an Expected value in statistics by hand

Watch the video for an case:

How to notice an Expected Value

Can't see the video? Click here.

This section explains how to figure out the expected value for a single item (like purchasing a single raffle ticket) and what to do if you accept multiple items. If yous have a detached random variable, read Expected value for a detached random variable.

Example question: You purchase ane $10 raffle ticket for a new automobile valued at $15,000. Two one thousand tickets are sold. What is the expected value of your gain?

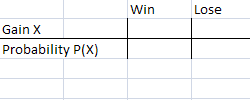
Footstep one: Make a probability nautical chart (see: How to construct a probability distribution). Put Gain(X) and Probability P(10) heading the rows and Win/Lose heading the columns.

Footstep 2: Figure out how much you could proceeds and lose. In our case, if we won, we'd exist upwardly $fifteen,000 (less the $ten cost of the raffle ticket). If you lose, you'd be downward $10.  Fill in the data (I'k using Excel here, so the negative amounts are showing in red).

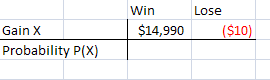
Step 3: In the bottom row, put your odds of winning or losing. Seeing as 2,000 tickets were sold, you have a one/2000 adventure of winning. And you too have a 1,999/2,000 probability chance of losing.

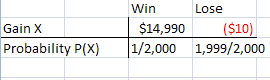
Step iv: Multiply the gains (X) in the top row by the Probabilities (P) in the bottom row.
$14,990 * 1/2000 = $7.495,
(-$x)*(1,999/2,000)= -$ix.995

Stride v:Add the 2 values together:
$7.495 + -$9.995 = -$2.5.

That's it!

Note on multiple items: for case, what if you purchase a $x ticket, 200 tickets are sold, and every bit well as a auto, you have runner up prizes of a CD histrion and luggage gear up?

Perform the steps exactly as above. Brand a probability nautical chart except y'all'll have more items:

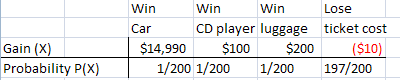
Then multiply/add the probabilities as in step iv: 14,990*(1/200) + 100 * (1/200) + 200 * (1/200) +  -$ten * (197/200).

You'll notation now that because you lot accept 3 prizes, you have 3 chances of winning, and then your chance of losing decreases to 197/200.

Note on the formula: The actual formula for expected gain is E(Ten)=∑X*P(X) (this is also one of the AP Statistics formulas).  What this is saying (in English) is "The expected value is the sum of all the gains multiplied by their individual probabilities."

Like the caption? Bank check out the Practically Cheating Statistics Handbook, which has hundreds more step-past-step explanations, just like this one!

Dorsum to Peak

Find an Expected Value in Excel

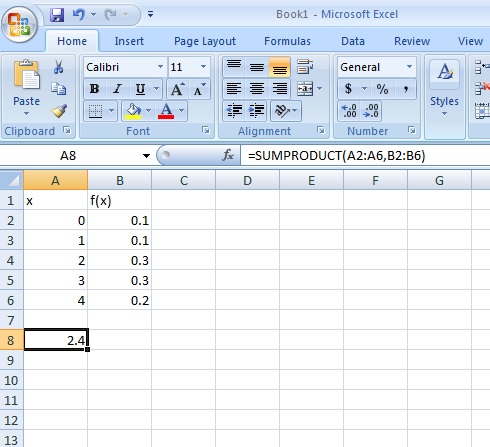
Step i: Type your values into two columns in Excel ("x" in i column and "f(x)" in the adjacent.
Step 2: Click an empty cell.
Step three: Type =SUMPRODUCT(A2:A6,B2:B6) into the jail cell where A2:A6 is the bodily location of your x variables and f(10) is the actual location of your f(x) variables.
Step four: Press Enter.

That's it!
Back to Meridian

Find an Expected Value for a Discrete Random Variable

You tin can think of an expected value equally a mean, or average, for a probability distribution. A discrete random variable is a random variable that can but have on a sure number of values. For example, if you were rolling a die, it tin only have the ready of numbers {one,2,iii,iv,5,6}. The expected value formula for a discrete random variable is:

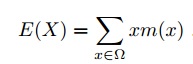
Basically, all the formula is telling yous to practise is observe the hateful by adding the probabilities. The mean and the expected value are and so closely related they are basically the aforementioned thing. You lot'll need to practice this slightly differently depending on if you accept a set of values, a set of probabilities, or a formula.

Expected Value Discrete Random Variable (given a list).

Case problem #one: The weights (X) of patients at a clinic (in pounds), are: 108, 110, 123, 134, 135, 145, 167, 187, 199. Presume one of the patients is chosen at random. What is the EV?

Stride 1: Notice the mean. The hateful is:
108 + 110 + 123 + 134 + 135 + 145 + 167 + 187 + 199 = 145.333.
That'due south it!

Expected Value Detached Random Variable (given "X").

Example trouble #2. You toss a off-white coin iii times. X is the number of heads which appear. What is the EV?
Step i: Effigy out the possible values for Ten. For a iii coin toss, yous could go anywhere from 0 to 3 heads. So your values for X are 0, 1, 2 and 3.

Step ii: Figure out your probability of getting each value of X. You may need to apply a sample space (The sample infinite for this problem is: {HHH TTT TTH THT HTT HHT HTH THH}). The probabilities are: i/8 for 0 heads, 3/8 for 1 head, 3/8 for two heads, and 1/eight for three heads.

Step 3: Multiply your 10 values in Stride 1 by the probabilities from stride ii.
E(X) = 0(1/8) + i(3/8) + 2(iii/eight) + 3(1/8) = three/2.

The EV is 3/2.

Expected Value Discrete Random Variable (given a formula, f(x)).

Example problem #3. You toss a money until a tail comes up. The probability density role is f(x) = ½^x. What is the EV?
Stride one: Insert your "ten" values into the get-go few values for the formula, one by one. For this particular formula, yous'll get:
1/2⁰ + 1/ii¹ + 1/2² + one/two³ + one/2^four + ane/2^five.

Stride ii: Add together up the values from Stride ane:
= i + ane/two + ane/iv + 1/8 + 1/16 + 1/32 = i.96875.

Note: What y'all are looking for here is a number that the series converges on (i.e. a set number that the values are heading towards). In this case, the values are headed towards 2, so that is your EV.

Tip: You can only use the expected value discrete random variable formula if your function converges absolutely. In other words, the function must terminate at a particular value. If it doesn't converge, then there is no EV.

Dorsum to Tiptop

What is Expected Value in Statistics used for in Real Life?

Expected values for binomial random variables (i.e. where y'all take ii variables) are probably the simplest type of expected values. In real life, you lot're likely to encounter more complex expected values that have more than than two possibilities. For case, you might buy a scratch off lottery ticket with prizes of $chiliad, $10 and $1. You might want to know what the payoff is going to exist if you get ahead and spend $i, $five or even $25.

Permit's say your school is raffling off a season pass to a local theme park, and that value is $200. If the schoolhouse sells i thousand $ten tickets, every person who buys the ticket will lose $9.lxxx, expect for the person who wins the season pass. That'south a losing proposition for you (although the school will rake it in). You might want to save your money! Here's the math behind it:

1. The value of winning the season ticket is $199 (you lot don't get the $10 dorsum that you lot spent on the ticket.
2. The odds that you win the season pass are 1 out of thousand.
3. Multiply (ane) by (2) to get: $199 * 0.001 = 0.199. Set this number bated for a moment.
4. The odds that you lose are 999 out of thou. In other words, your odds of ending up minus ten dollars are 999/chiliad. Multiplying -$10, you go -9.999.
5. Adding (3) and (iv) gives us the expected value: 0.199 + -9.999 = -ix.80.

Here'south that scenario in a tabular array:

St Petersburg Paradox

What is the Saint petersburg Paradox?

The St. petersburg Paradox has been stumping mathematicians for centuries. It'due south almost a betting game you can always win. But despite that fact, people aren't willing to pay much money to play it. Information technology's called the St. Petersburg Paradox because of where it appeared in print: in the 1738 Commentaries of the Imperial Academy of Scientific discipline of St. petersburg.

The Paradox is this: At that place's a elementary betting game you tin can play where your winnings are always going to be bigger than the amount of money y'all bet. Imagine buying a scratch off lottery ticket where the expected value (i.e. the amount you can expect to win) is ever college than the amount you pay for the ticket. Y'all could purchase a ticket for $1, $x, or a million dollars. You will always come upwardly alee. Would you lot play?

Assuming the game isn't rigged, you probably should play. Simply the paradox is that about people wouldn't be willing to bet on a game similar this for more than a few dollars. So, why is that? There are a couple of possible explanations:

1. People aren't rational. They aren't willing to adventure their money even for a sure bet.
2. In that location has to be something incorrect with the game'due south odds. Surely the odds of winning tin't always be that good, can they?

The short answer is, people are rational (for the well-nigh part), they are willing to part with their money (for the most part). And, at that place is admittedly zero wrong with the game. If you lot're confused at this indicate — that is why it's called a paradox.

The St. petersburg Paradox Game.

How much would y'all bet if you could always win?

The original paradox wasn't near lottery tickets (they didn't exist in 1738). It was virtually a money toss game. Suppose you were asked past a friend to play a coin toss game for $ii. Assume the coin is off-white (i.e. it isn't weighted). You toss the coin until the first tails comes up, at which time you lot would earn $2ⁿ and the game would terminate. In other words, if tails come up up on the outset toss, yous would win $ii^ane = $2. If tails comes up on the tertiary toss, you would win $2^three = $viii. And if you had a run and tails showed upwards on the 20th toss, you would win $ii²⁰ = $one,048,576.

If you figure out the expected value (the expected payoff) for this game, your potential winnings are infinite. For example, on the first flip, you have a 50% chance of winning $2. Plus you get to toss the coin again, then yous also have a 25% hazard of winning $4, plus a 12.5% take chances of winning $8 and and so on. If you bet over and once again, your expected payoff (gain) is $1 each time you play, every bit shown by the following table.

P(northward)	Prize	Expected payoff
1	one/2	$2	$1
2	1/4	$4	$1
3	1/8	$8	$1
4	1/16	$16	$one
5	1/32	$32	$i
half dozen	1/64	$64	$i
7	1/128	$128	$ane
8	1/256	$256	$1
9	1/512	$512	$1
10	1/1024	$1024	$1

You can't possibly lose money. Still, despite the expected value being infinitely big, most people wouldn't be willing to fork out more than a few bucks to play the game.

The St. Petersburg paradox has been debated by mathematicians for about three centuries. Why won't people risk a lot of coin if the odds are certainly in their favor? Equally of yet, no 1 has found a satisfactory respond to the paradox. As Michael Clark states: "[The St. Petersburg Paradox] seems to exist 1 of those paradoxes which nosotros accept to eat." A couple of solutions, which accept been presented and all the same have failed to offering a satisfactory answer:

• Limited utility (suggested by Jacob Bernoulli). Basically, the more than nosotros have of something, the less satisfied we are with it. You tin apply this to candy; You're probable to be satisfied with 1 bag, but after six or 7 bags, you're likely to not want any more. All the same, y'all tin can't utilise this to money. Anybody wants more coin, correct?
• Risk aversion. The average person might consider putting a few one thousand dollars in the stock market. Merely they wouldn't be willing to gamble their entire life savings. Yous tin't apply this rule to the St. Petersburg Paradox game considering there is no risk.

Next: Powerball Expected Value

References

Clark, Michael, 2002, "The Petrograd Paradox", in Paradoxes from A to Z, London: Routledge, pp. 174–177.
Papoulis, A. "Expected Value; Dispersion; Moments." §5-iv in Probability, Random Variables, and Stochastic Processes, 2nd ed. New York: McGraw-Hill, pp. 139-152, 1984.

Related manufactures:
Online expected value calculator.

---------------------------------------------------------------------------

Need aid with a homework or test question? With Chegg Study, you can get step-past-step solutions to your questions from an expert in the field. Your first 30 minutes with a Chegg tutor is complimentary!

Comments? Need to mail a correction? Please post a annotate on our Facebook page .

sancheznamintaid.blogspot.com

Source: https://www.statisticshowto.com/probability-and-statistics/expected-value/

Share this post